At the heart of KID-PPG lie three key insights on PPG, Heart Rate and motion artifacts:
- Motion artifact removal needs to be explicitely defined as a source separation task.
- In certain cases the PPG might be so corrupted by motion that it is infeasible to recover the heart rate from it – even if we have access to acceleration information through accelerometer sensors.
- The Blood Volume Pulse has specific characteristics. For example we saw in the introduction that a clean PPG signal is composed of the 2 • HeartRate components.
We have designed three mechanisms to integrate this prior-knowledge into KID-PPG:
- Explicit Source Separation
- Probabilistic Inference and
- Guided Training
We detail these three mechanisms below, providing also details on how our kid-ppg python package can be used for direct heart rate estimation using these three key insights.
Our python kid-ppg package is the first ever PPG-based heart rate extraction deep learning model with publicly available pretrained weights. You can easily install it and start analyzing PPG and acceleration data by simply downloading it through pip:
pip install kid-ppg
1. Explicit Source Separation
As we’ve seen, external motions can significantly damage the heart component in the PPG signal. In the case of periodic motions we can get some hints about the motion artifacts by observing the acceleration signals. In this case the 3D acceleration signal acts as a motion reference which we utilize to cancel the motion artifacts from the PPG.
Unlike the SoA Deep Learning PPG models, which perform arbitrary data fusion, we propose an explicit source separation task. This way we enable the model to only focus on the most relevant parts of the signal – the Blood Volume Pulse.
We chose to implement this source separation task as a linear adaptive filter. kid-ppg provides the AdaptiveFilteringModel for linear adaptive filtering. Calling an AdaptiveFilteringModel model first trains the model adaptively based on the input PPG and accelerations. Then, it performs filtering based on the learned weights.
import tensorflow as tf
from kid_ppg.preprocessing import sample_wise_z_score_normalization, sample_wise_z_score_denormalization
from kid_ppg.adaptive_linear_model import AdaptiveFilteringModel
# We define an optimizer which we will use to converge
# the adaptive model.
sgd = tf.keras.optimizers.legacy.SGD(learning_rate = 1e-7,
momentum = 1e-2,)
# We train the model for 1000 epochs.
n_epochs = 1000
model = AdaptiveFilteringModel(local_optimizer = sgd,
num_epochs_self_train = n_epochs)
# We simultaneously perform model training and
# filtering. X_input contains the PPG signals in
# its first channel and 3 acceleration signals
# in the rest 3 channels. Overall, X_input size
# is [N_samples, 256, 4].
PPG_filtered = model(X_input[..., None]).numpy()
The resulting PPG_filtered contains the the PPG signal after removing the motion artifacts. The results of our exploration showcase how this explicit source separation can significantly boost the performance of multiple deep learning models.
Filtered PPG Signal
Motion Artifacts Q-PPG
Filtered PPG Q-PPG
Figure 5: PPG and Heart Rate Extraction with and without adaptive linear filtering.
2. Probabilistic Inference
Unfortunately, acceleration is not always enough to cancel the effect of motion artifacts and get an accurate HR. In many cases, e.g. random motion, the acceleration does not provide any additional information for the motion. Additionally, the artifacts may be strong enough to completely corrupt the PPG signal beyond any capability of recovery. In our analysis we have found out that for a significant portion of the PPGDalia dataset none of the currently available methods (Signal Processing or Deep models) can robustly recover the HR.
In these cases, since the model does not have access to relevant information (destroyed BVP), any heart rate estimation might be untrustworthy. Preferably, we would like it to respond with “I do not know, I cannot see the BVP clearly” when asked about the heart rate.
One way to introduce this “I don’t know” capability to the model is through probabilistic output. With a probabilistic output, the model does not output one single HR estimation, but rather a distribution of heart rates. An output distribution with a wide range of plausible heart rates (e.g. from 65 BPM to 150 BPM) indicates an uncertain HR estimation – the model cannot easily dissern the required BVP component in the input. Conversely, if the output heart rate distribution is concentrated around an HR value (e.g. from 65 BPM to 67 BPM), then the model is certain of its output.
KID-PPG defines this distribution as a Gaussian. This allows us to describe the distribution using only the expected output (most probable heart rate) and standard deviation (which relates to the range of probable heart rates): N(μhr,σ2hr). μhr expresses the most probable heart rate, while σhr is related to the spread of the range of probable heart rates.
Let’s see an example of probabilistic inference on the examples of Figures 2 and 3:
Figure 4: Example of probabilistic inference on clean and motion-artifact affected signals. We present the energy of each sample as calculated by the Fourier transform. The range of possible heart rates, KID-PPG output, is presented as the shaded area. Left: KID-PPG is performing heart rate extraction on the clean sample of Figure 2. It has estimated that the heart rate is probably located around 82 BPM. The blue circle at 82.5 BPM indicates the true heart rate as measured by ECG. Right: We then perform probabilistic heart rate extraction in the corrupted sample of Figure 3. Since the PPG is seriously corrupt, KID-PPG outputs a large range of potential heart rates – essentially indicating “I don’t know”. The true heart rate is also presented with an orange circle. We also contrast KID-PPG output with the output of another deep learning model, which does not perform probabilistic inference (Q-PPG) with a black vertical line.
We can easily perform probabilistic HR estimation using the kid-ppg package. All we need is to instantiate a KID_PPG() model and perform a prediction using the model’s predict() function:
from kid_ppg.kid_ppg import KID_PPG
from kid_ppg.preprocessing import create_temporal_pairs
# The KID-PPG model receives inputs as pairs [PPG(t - 1), PPG(t)]
# The kid-ppg package provides a utility function to easily form
# these pairs.
X_filtered_temp, y_temp = create_temporal_pairs(X_filtered, y)
# Instantiate a KID_PPG model.
kid_ppg_model = KID_PPG()
# Perform prediction on the temporal PPG samples.
hr_pred_m, hr_pred_std = kid_ppg_model.predict(X_filtered_temp)
The predict function returns the expected HR values, μhr and the standard deviations, σhr, corresponding to the input PPG samples, X_filtered_temp.
The standard deviation, hr_pred_std, provides a soft label which can be considered as the model’s certainty on its HR estimation. Using the standard deviation we can tell if one sample is more uncertain than another one. However, in many applications we want our model to not exceed a maximum error of heart rate estimation. KID-PPG allows to define such a threshold and retain only the samples which present a low probability of exceeding this error threshold.
For example, let’s consider that for our application specifies a maximum estimation error of 10 BPM. We can use the output distribution, N(μhr,σ2hr) to classify each sample as “probably high-error” (probably error > 10BPM) or “probably low-error” (probably error < 10BPM). Similarly to predict, we use predict_threshold, but here we also define the threshold parameter:
Along with the hr_pred_m and hr_pred_std, this time we also get hr_pre_p, which is the probability the estimation error will not exceed the defined threshold. We can then retain only the samples which have a hr_pred_p higher than 0.5.
3. Guided Training
Probabilistic output allows the model to output “I don’t know”. Without any guidance the model can converge to a lot of different rules on what it believes a “clean” sample or a damaged beyond any recovery are. For example if the majority of clean training samples are of low energy, then the model could learn the shortcut: “When the PPG signal energy is low, I am certain”. Of course, we know that this rule is not robust: low energy signal could still mean no Blood Volume Pulse in the input. Let’s do a small experiment, Figure 6. We select a clean PPG sample and corrupt it beyond any possibility for recovery by filtering-out the portion of the signal which corresponds to the heart rate:
Let’s do a small experiment, Figure 6. We select a clean PPG sample and corrupt it beyond any possibility for recovery by filtering-out the portion of the signal which corresponds to the heart rate: energies at HeartRate, 2 • HeartRate and 3 • HeartRate. Without any guidance during training, probabilistic model outputs a low-uncertainty output.
We then boost KID-PPG’s robustness in uncertainty estimation. We guide the model to base its uncertainty based on our prior-knowledge of a clean PPG signal – containing the HeartRate, 2 • HeartRate and maybe 3 • HeartRate in very good cases. We achieve this by complementing the training dataset with synthetically corrupted realistic samples and guiding the model to be uncertain of them.
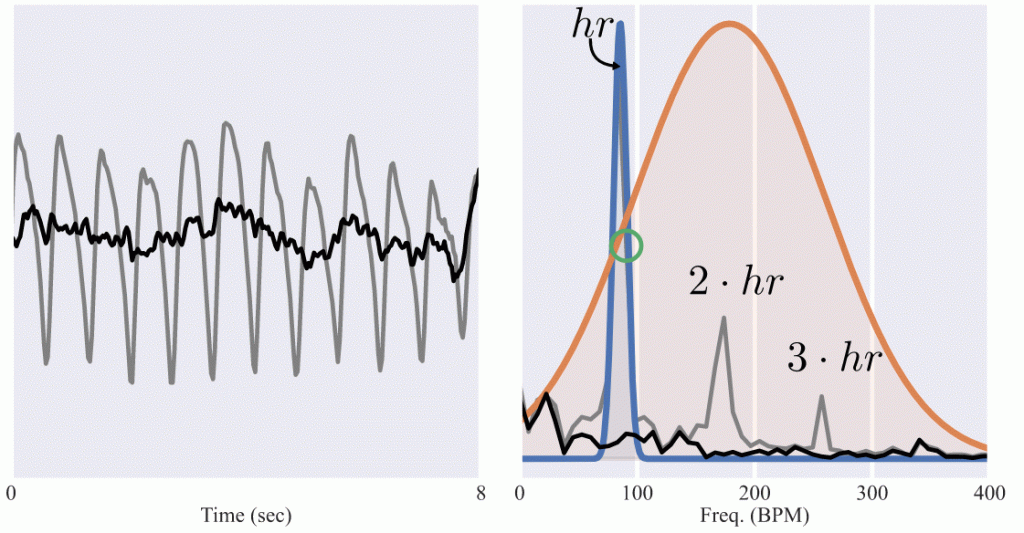
Figure 6: Robust uncertainty estimation can be benefited by guided training based on prior-knowledge on the expected morphology of clean PPG signals. Left: We corrupt a clean sample (grey) by removing the heart component out of it (black). Right: The energy vs frequency plots of the clean (grey) and corrupted signals (black). The ground-truth heart rate is presented with a green circle. The unguided model presents a low uncertainty (blue), even though the signal is heavily corrupted to the point of no reconstruction. In contrast, KID-PPG, which is guided during probabilistic training, is uncertain of its output.
Our results indicate that guided probabilistic training boosts the model’s robustness in estimating the probability of its estimations’ error.
Our analysis has also revealed that the range of heart rates available in the training dataset will affect the end-result model. For example, let’s consider training data with HR in the range of [50, 150] BPM. A model trained on these data will not learn to identify faster heart rates, for example at 200 BPM. As far as this model is concerned, the HR is always in the range of [50, 150] BPM. However, through medical knowledge we are sure that human heart rate can exceed the 150 BPM limit of the training data. This is why in KID-PPG we make sure the training set contains samples from the entire range of possible human heart rates. Since real recorded data might not be able to provide this vast range, we have synthetically enriched the training set.
Let’s see an example of the advantage of guiding the network to consider a wider range of heart rates.
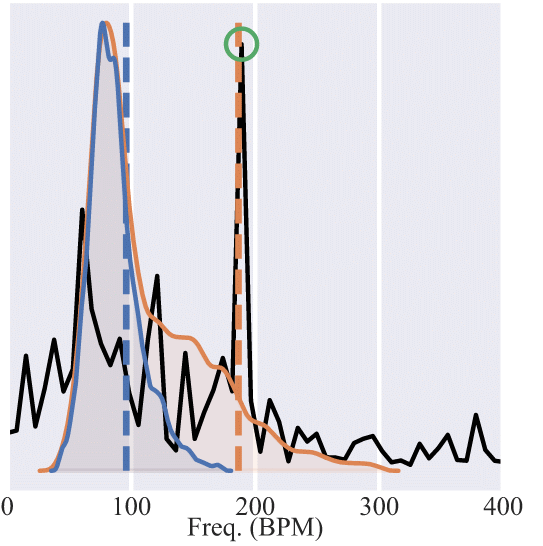
Figure 7: Demo of the effect of the heart rate range in the training samples. The Fourier transform of signal is presented in black and the green circle signifies the ground-truth heart rate. The frequency corresponding to the heart rate presents a distinguishable peak, and extracting the heart rate is straightforward for this sample. When trained on a limited range of heart rates (blue distribution) the model predicts a considerably lower heart rate (blue vertical line), even though it should be quite easy to detect the correct periodicity. We then synthetically expand the range of the original training set to include the entire range of humanly possible heart rates (orange distribution). The guided model then predicts correctly the heart rate.
Open Source Pretrained KID-PPG
You can directly use our pretrained KID-PPG model using our pypi package available here. You can also check our KID-PPG manuscript. Finally, check-out our end-to-end kid-ppg workflow in this tutorial notebook.